Մենք վստահ ենք, որ դուք կսխալվեք. մաթեմատիկական ակնարկ՝ «քթածակով» մարդկանց համար

Մոտավեր քանի՞ մարդ է պետք պատահականության սկզբունքով ընտրել, որ նրանից գոնե երկուսը 99.9% հավանականությամբ նույն օրը ծնված լինեն։ (Մարդիկ ընտրվում են ամբողջովին պատահական և տարբավ բոլոր օրերը հավասարահավանական ծննդյան օրեր են)

Պետք չէ երկար մտածել այս մասին, այլ պետք է պարզապես մոտավոր թիվ ասել։ Սա ստուգում է Ձեր հոտառությունը կամ «քթածակ» ունենալը։

Զարմանալի չէ, որ մարդկանց ծանրակշիռ մեծամասնությունը ասեում է 250 կամ ավելի։ Եվ իսկապաես, բավականին շատ մարդ է պետք վերցնել, որ նրանցից գոնե երկուսը 99.9% հավանականությամբ նույն օրը ծնված լինեն։

Սակայն մաթեմատիկան փաստում է, որ այդ մարդկանց մեածամասնությունը սխալվում է։ Բանն այն է, որ առնվազն երկու հոգու ծնունդների այդպիսի հավանականությամբ համընկնում ունենալու համար անհրաժեշտ է ընտրել ընդհամենը 70 հոգում։

Ստորև ներկայացնում ենք նաև այդ խնդիր մաթեմատիկական լուծումը՝ օգտագործելով հակառակ տրամաբանություն։ Եկեք սկսեքն հաշվարկը, որի օգնությամբ կպարզենք, թե ինչքան է այն հավանականությունը, որ 70 հոգուց կզամված խմբում նույնիսկ երկու հոգի չեն ծնվել նույն օրը( սա նշանակում ենք P(A’))։ Այդպես մենք ավելի հեշտացնում ենք հաշվարկը, քանի որ հետո կարող ենք պարզապես 100% -ից հանել ստացված թիվը և պարզել այն հավանականությունը, որով 70 հոգանոց խմբում առնվազն երկու հոգի ծնվել են նույն օրը(իսկ սա նշանակում ենք P(A))։

հաշվարկի համար ընդունում ենք, որ տարին ունի 365 օր, որոնցից բոլորը հավասարահավանական ծննդյան օրեր են։ (P(A) + P(A’) = 1)

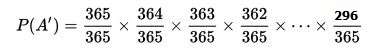
Էլ ավելի պարզեցնելով հավասարումը կստանանք, որ 

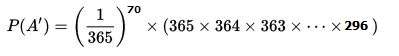
Հաշվելով սա մենք ստանում ենք, որ P(A’) ≈ 0.001,

Ինչպից էլ հետևում է, որ P(A) ≈ 0.999 => 99,9%